„Die Summe der ersten bla natürlichen Zahlen“ oder „Die Summe der Quadrate der ersten bla natürlichen Zahlen“, Strukturen, mit denen man nur ungern rechnet. Gut, dass man Formeln daraus machen kann, aber wie macht man sich die begreiflich?
Fangen wir mal mit der 26 an, was soll die denn da? Ich habe die beiden Nenner „2 und 6“ der hier beschriebenen Summenformeln einfach zusammengefasst. Es entsteht die 26, die Nummer des Tages jenes Monats in der Vergangenheit, an dem ich das Licht der Welt erblickte. Und die Gotteszahl! Ich erkläre es. Im Hebräischen stellt jedes Wort gleichzeitig eine Zahl da. Dem hebräischen Wort für Jahwe, also Gott, wird die Zahl 26 zugeordnet. 26 ist aber die 2 x 13 und den hebräischen Wörtern für „Einheit“ und „Liebe“ wird jeweils die Zahl 13 zugewiesen. Gott ist demnach also Einheit UND Liebe, nicht nur eins davon, Polarität statt Dualität, Yin und Yang sozusagen. Zurück in die mathematische Gegenwart.
Wie stellt man eine Formel auf, die die ersten n natürlichen Zahlen aufsummiert? Man liest alte Geschichten von Carl Friedrich Gauß! Eine davon spiegelt so manchen Unterricht von heute wider. Der Mathelehrer hat irgendwie keine Lust auf Unterricht und beschließt, die Schüler zu beschäftigen. Er erteilt die Aufgabe, die natürlichen Zahlen zwischen 1 und 100 zu addieren. Die Hoffnungsblase, eine halbe Stunde aus dem Fenster schauen zu können, platzt nach wenigen Sekunden. Der gute Gauß steht auf und schreibt 5050 an die Tafel. Gauß konnte noch nicht googlen, wie hat er das also gemacht?
Er sieht sich die Zahlenreihe an. Am Anfang die 1 und am Ende die 100. Die zweite Zahl ist die 2 und die vorletzte die 99. Das war es schon. Von außen nach innen ergibt die Summe der Zahlenpaare immer 101. Beim Pärchen 50-51 angekommen sind alle Zahlen abgearbeitet. 50 Pärchen zu je 101, das wird multipliziert und das Ergebnis ist 5050. Fertig! Solche Schüler wünscht man sich doch, oder?
Wenn man dieses Beispiel auf die Summe der ersten 1000 natürlichen Zahlen bringt, muss man halt 500 mal 1001 rechnen und kommt auf 500500. Das scheint zu funktionieren. Ersetzt man die 1000 durch „n“, muss man demnach „n+1“ (also 1000+1) mit n-halbe (500) multiplizieren. Es entsteht die Formel „n * (n+1) durch 2“. Das sind die Momente, da flippt ein Mathematikfreund innerlich total aus, er zeigt das nicht, aber das ist wie Bungee-Jumping vom Burj Khalifa.
Diese Formel, die nach Gauß benannt wurde – Kleiner Gauß – kann man auch zeichnen. Schaut mal oben auf das große Bild. Wenn man die Zahlen 1,2,3,4,5… als Kästchen malt und Reihe für Reihe ein Kästchen mehr zeichnet, dann entsteht ein Dreieck von Kästchen und die Summe der Kästchen entspricht der Summe der ersten n natürlichen Zahlen. Nimmt man nun das so erhaltene Dreieck und dreht es um 180 Grad, kann man es auf das ursprüngliche Dreieck draufsetzen. Es entsteht ein Rechteck. Die Breite ist „n“ und die Höhe einen mehr, also „n+1“. Die Fläche des Rechtecks ist aber Breite mal Höhe oder eben „n * (n+1)“. Das Dreieck ist aber genau die Hälfte von jenem Rechteck, also das Ganze durch 2 und wir haben den kleine Gauß zeichnerisch nachgewiesen.
Gehen wir einen Schritt weiter. Die Summe der ersten n Quadrate von natürlichen Zahlen müsste wohl auch eine Summenformal besitzen, tut sie auch: n * (n+1) * (2n+1) und das Ganze durch 6 geteilt. Wie kommt man jetzt dahin?
Wir führen die Idee einfach konsequent weiter. Wenn man für die Summe von Zahlen in der ersten Potenz 2 Dimensionen zum Zeichnen braucht, wird man wohl die Summe von Zahlen in der zweiten Potenz 3 Dimensionen brauchen. Schaut Euch mal im großen Bild diese seltsame Viertelpyramide an. Wenn Ihr die Anzahl der Würfel pro Schicht zählt, kommt ihr auf: 1, 4, 9, 16, 25… Das sind aber genau die Quadrate der natürlichen Zahlen. Und wenn man diese Würfel aufaddiert, hat man die Summe der ersten n Quadratzahlen. Warum muss man in der Formel aber durch 6 teilen?

Aus 6 Viertelpyramiden… 
…wird ein Quader.
Zur Beantwortung gehen wir mal die Sache von der anderen Seite aus an: n * (n+1) * (2n+1), drei Zahlen miteinander multipliziert, das hört sich schwer nach dem Volumen eines Quaders an. Das Volumen wird durch 6 geteilt. Es scheint so, als wäre der Quader aus 6 gleichgroßen Körpern zusammengebaut. Und diese Körper? Na, das scheinen unsere Viertelpyramiden zu sein. Es ist Zeit, um zu experimentieren. Packt mal Euer Lego aus. Ich habe das auch gemacht und sechs dieser Viertelpyramiden nachgebaut. Farblich ist das jetzt nicht der Brüller, aber bei Lego gilt immer: Egal, was Du bauen willst, Du hast nie genau die Steine, die Du brauchst. Die beiden Bilder oben zeigen die 6 Viertelpyramiden einzeln und zusammengebaut. Das funktioniert! Hier funkt es mit drei Ebenen, mit zwei geht es auch! Nehmt einfach die unterste Schicht ab und setzt die übrig gebliebenen Pyramiden zusammen. Sollte ich in dem Durcheinander von Legosteinen genügend weitere finden, damit ich 6 Pyramiden mit der Schichtgröße von 4 bauen kann, packe ich die Bilder hier rein. Wenn Ihr die Beweistechnik der vollständigen Induktion beherrscht, dann könnt Ihr ohne weiteres Bauen auch nachweisen, dass das mit 45 Schichten klappt.
Nachdem wir nun gezeigt haben, dass sich das Aufbewahren der alten Legos unbedingt lohnt, werfen wir einen verstohlenen Blick auf die Summe der ersten n natürlichen Zahlen in der dritten Potenz. Auch das geht, dazu müssen wir aber vierdimensionale Legosteine haben. Ich habe die leider nicht mehr, sollte aber jemand noch eine Kiste davon besitzen, baut das mal zusammen und schickt mir Fotos davon!
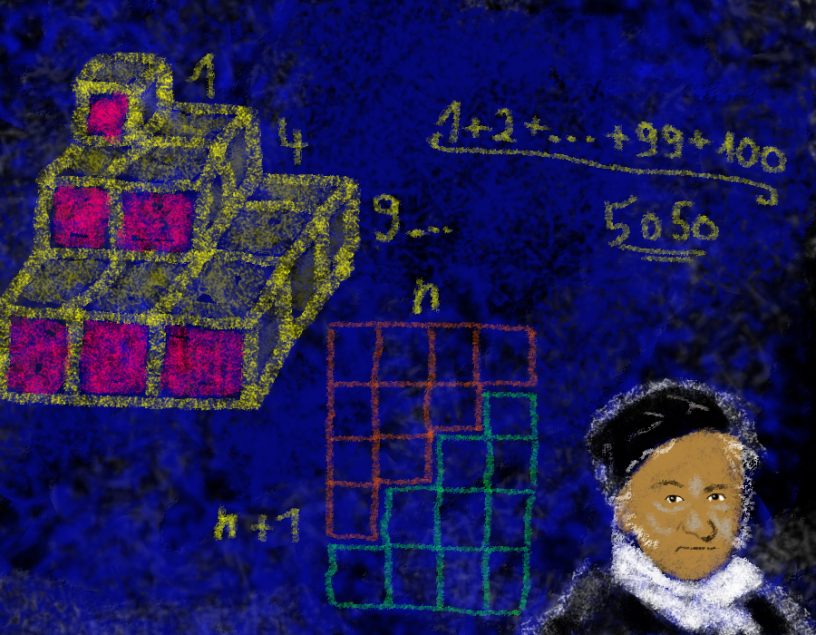






Anonym
Es lohnt sich also doch, Lego zu sammeln